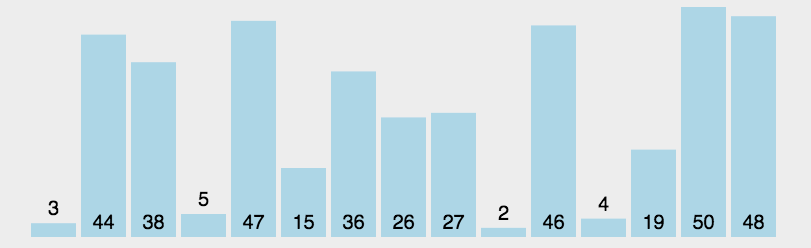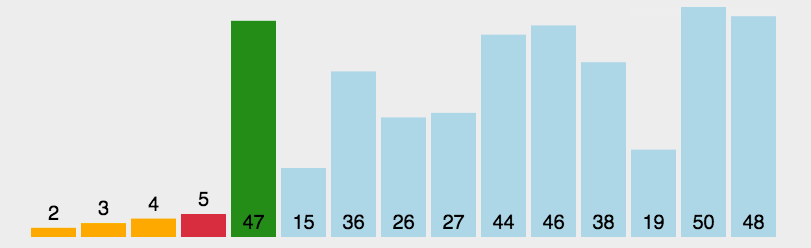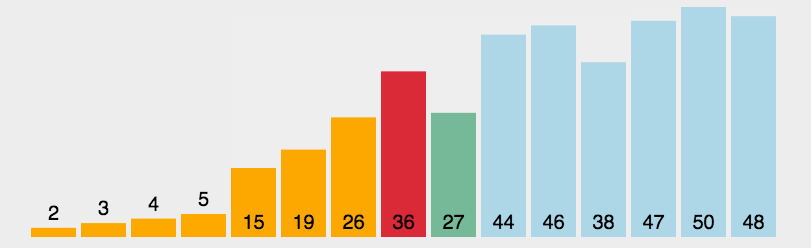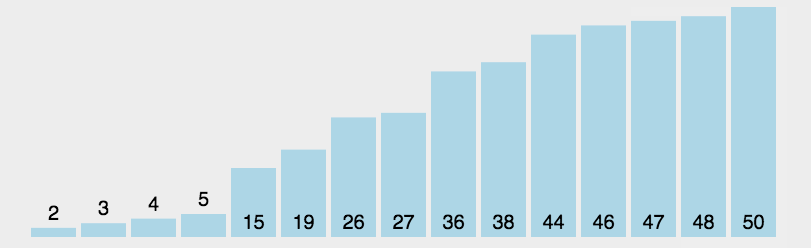
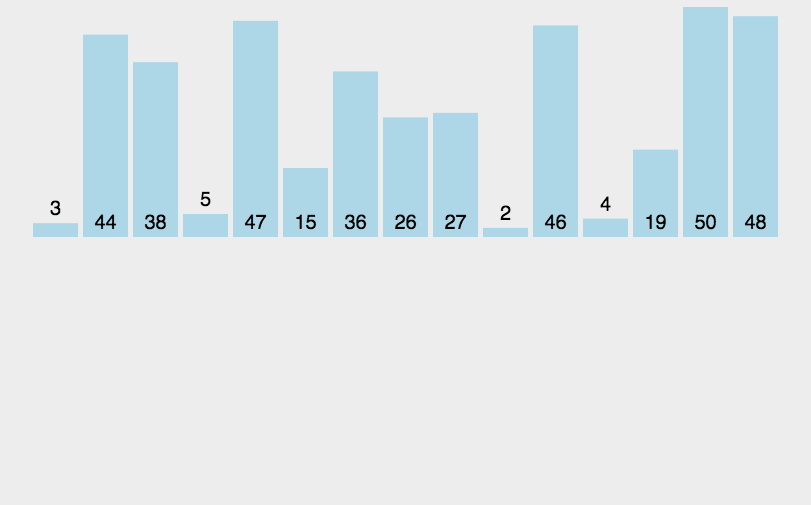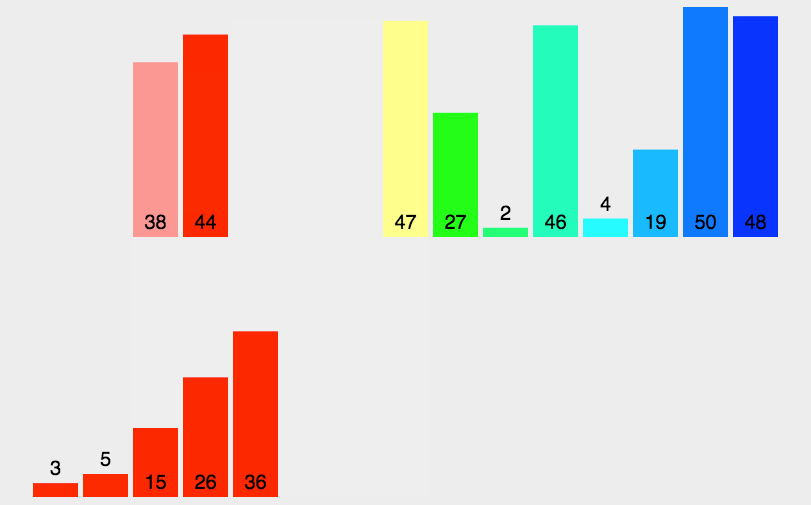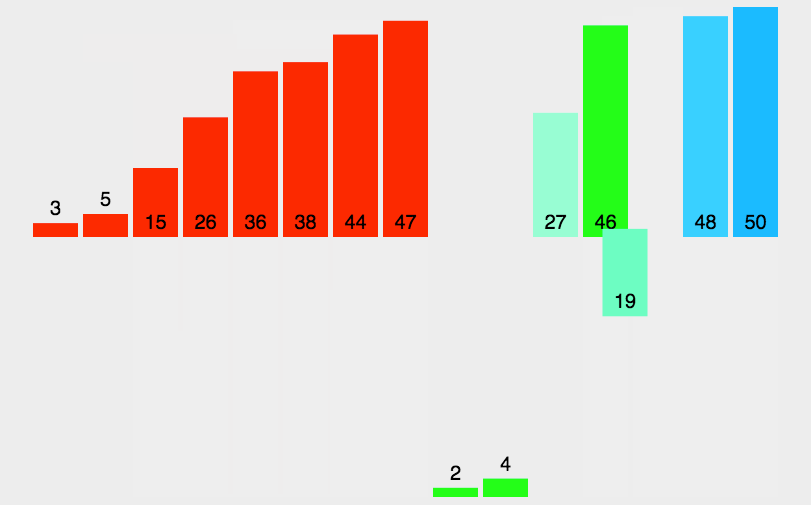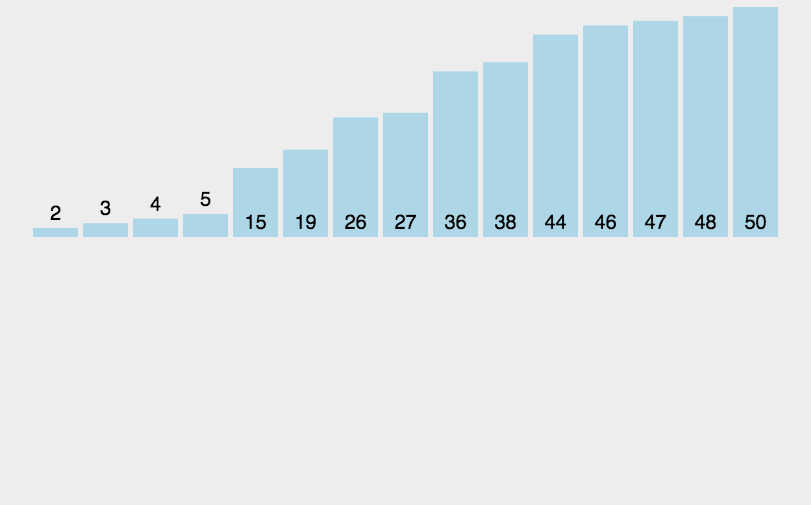
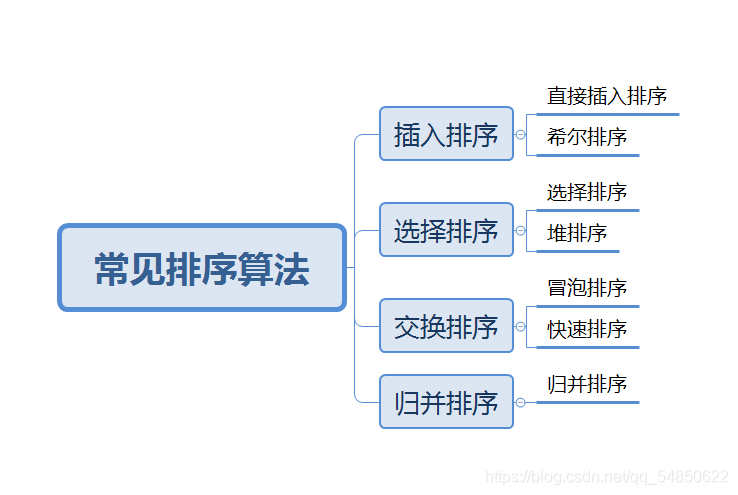
排序的种类 排序分为内部排序 和外部排序
一般为内部排序,可以划分为八大排序
八大排序算法是:1、直接插入排序;2、希尔排序;3、简单选择排序;4、堆排序;5、冒泡排序;6、快速排序;7、归并排序;8、桶排序/基数排序。
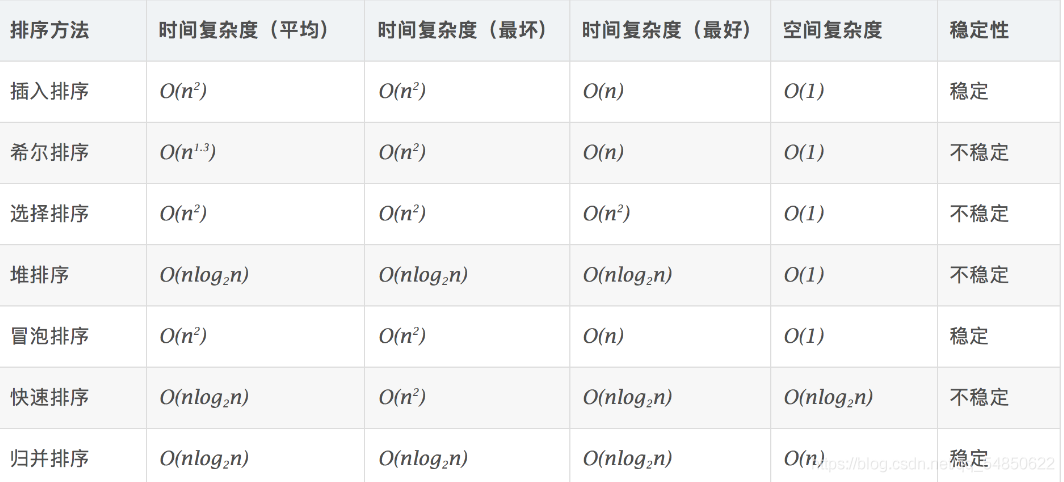
排序算法的稳定性 假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i] = r[j],且 r[i] 在 r[j] 之前,而在排序后的序列中,r[i] 仍在 r[j] 之前,则称这种排序算法是稳定的;否则称为不稳定的。
冒泡排序中,只有左边的数字大于右边的数字时才会发生交换,相等的数字之间不会发生交换,所以它是稳定的。
而选择排序中,最小值和首位交换的过程可能会破坏稳定性。比如数列:[2, 2, 1],在选择排序中第一次进行交换时,原数列中的两个 2 的相对顺序就被改变了,因此,我们说选择排序是不稳定的。
直接插入排序 思想:将一个数组中的数据看作两个数组,有序和无序数组,由于第一个无需比较,所以需要比n-1次,将无需数组的第一个与有序数组的最后一个依次对比,并且插入合适的位置
1 2 3 4 5 6 7 8 9 10 11 12 void InsertSort (int arr[]) int len = arr.size (); for (int i = 0 ; i < len - 1 ; i++) { int next = arr[i + 1 ]; int index = i; while (index >= 0 && next < arr[index]) { arr[index + 1 ] = arr[index]; index --; } arr[index + 1 ] = next; } }
希尔排序 如果存在一个数组为{2,3,4,5,6,1}那么使用直接插入排序会导致算法效率很慢
所以说是对插入排序的一种优化,它是分组对每组进行排序,又叫做缩小增量排序
为什么希尔排序效率更高
由于开始时,步长的取值较大,每个子序列中的元素较少,排序速度较快,到排序后期步长取值逐渐变小,子序列中元素个数逐渐增多,但由于前面工作的基础,大多数元素已经基本有序,所以排序速度仍然很快。就是判断的多了,移动的次数变少,所以速度变快。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 void ShellSort (int arr[]) for (int gap = arr.size () / 2 ; gap > 0 ; gap /= 2 ) { int len = arr.size (); for (int i = gap; i < len; i++) { int index = i; int now = arr[index]; if (now < arr[index - gap]) { while (index - gap >= 0 && now > arr[index - gap]) { arr[index] = arr[index - gap]; index -= gap; } a[index] = now; } } } }
选择排序 简单选择排序 思想:将数组中的数据遍历,先拿第一个进行比较,看后面的有没有比这更小的,有的话交换,没有就第二个进行比,依次比较,一共需要比数组大小-1次 。第i 次排序后序列的前i 项都会变得有序。
1 2 3 4 5 6 7 8 9 void SelectSort (int arr[]) int len = arr.size (); for (int i = 0 ; i < len - 1 ; i++) for (int j = i + 1 ; j < len; j++) if (a[i] > a[j]) swap (a[i], a[j]); }
二元选择排序————简单选择排序的改进 简单选择排序,每趟循环只能确定一个元素排序后的定位。我们可以考虑改进为每趟循环确定两个元素(当前趟最大和最小记录)的位置,从而减少排序所需的循环次数。改进后对n个数据进行排序,最多只需进行[n/2]趟循环即可
1 2 3 4 5 6 7 8 9 10 11 12 13 void SelectSort (int arr[]) int len = arr.size (); for (int i = 0 ; i <= len / 2 ; i++) { int maxIndex = i; int minIndex = i; for (int j = i; j < len - i; j++) { if (a[j] > arr[maxIndex]) maxIndex = j; if (a[j] < arr[minIndex]) minIndex = j; } swap (a[i], arr[minIndex]); swap (a[j], arr[maxIndex]); } }
堆排序 大根堆,从小到大排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 void adjustHeap (int arr[], int i, int length) int temp = arr[i]; for (int k = 2 * i + 1 ; k < length; k = k * 2 + 1 ) { if (k + 1 < length && arr[k] < arr[k + 1 ]) k++; if (arr[k] <= temp) break ; arr[i] = arr[k]; i = k; } arr[i] = temp; } void HeapSort (int arr[], int size) for (int i = size / 2 - 1 ; i >= 0 ; i--) { adjustHeap (arr, i, size); } for (int j = size - 1 ; j > 0 ; j --) { swap (arr[0 ], arr[j]); adjustHeap (arr, 0 , j); } }
冒泡排序 思想:从前向后遍历, 每次判断相邻两数是否前数小于后数, 不满足则交换两数, 直到不需要交换为止
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 void BubbleSort (int arr[], int size) for (int i = 0 ; i < size - 1 ; i ++) { int count = 0 ; for (int j = 0 ; j < size - 1 - i; j ++) { if (arr[j] > arr[j + 1 ]){ arr[j] ^= arr[j + 1 ] ^= arr[j] ^= arr[j + 1 ]; count = 1 ; } } if (!count) return ; } }
快速排序 先找一个基准值 ,一般为数组大小/2,左边找到一个比基准值大的数,右边找到一个比基准值小的数,然后进行交换,算完之后左边的都为比基准值小的,右边都为比基准值大的,但不能保证他们是有序的,所以还需要对左右生成的数据进行二次排序,通过不断递归使得整个数组有序。
1 2 3 4 5 6 7 8 9 10 11 12 void QuickSort (int arr[], int l, int r) if (l >= r) return ; int i = l, j = r, key = l; while (i < j) { while (i < j && arr[key] <= arr[j]) j --; while (i < j && arr[i] <= arr[key]) i ++; swap (arr[i], arr[j]); } swap (arr[i], arr[key]); QuickSort (arr, l, i - 1 ); QuickSort (arr, i + 1 , r); }
快速选择:第K大数 基于快速排序思想,通过基准数的位置找出第K大数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 int QuickSelect (vector<int >& nums, int k, int l, int r) if (l >= r) return nums[l]; int i = l, j = r, key = (l + r) >> 1 ; swap (nums[l], nums[key]); while (i < j) { while (i < j && nums[j] <= nums[l]) j--; while (i < j && nums[i] >= nums[l]) i++; swap (nums[i], nums[j]); } swap (nums[l], nums[i]); int loc = i + 1 ; if (k > loc) return QuickSelect (nums, k, i + 1 , r); if (k < loc) return QuickSelect (nums, k, l, i - 1 ); return nums[i]; }
归并排序 利用完全二叉树特性,把数组递归拆成左右两个大小几乎相等部分,直到左右两部分不能再次拆分,深度相同的相邻左右子部分合并,直到整个数组有序,一共需要进行logn次合并和拆分。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 void Merge (int arr[], int temp[], int l, int mid, int r) int i = l, j = mid + 1 , k = l; while (i != mid + 1 && j != r + 1 ) { if (arr[i] <= arr[j]) temp[k ++] = arr[i ++]; else temp[k ++] = arr[j ++]; } while (i != mid + 1 ) temp[k ++] = arr[i ++]; while (j != r + 1 ) temp[k ++] = arr[j ++]; for (i = l; i <= r; i++) arr[i] = temp[i]; } void MergeSort (int arr[], int temp[], int l, int r) if (l >= r) return ; int mid = l + (r - l) / 2 ; MergeSort (arr, temp, l, mid); MergeSort (arr, temp, mid + 1 , r); Merge (arr, temp, l, mid, r); }
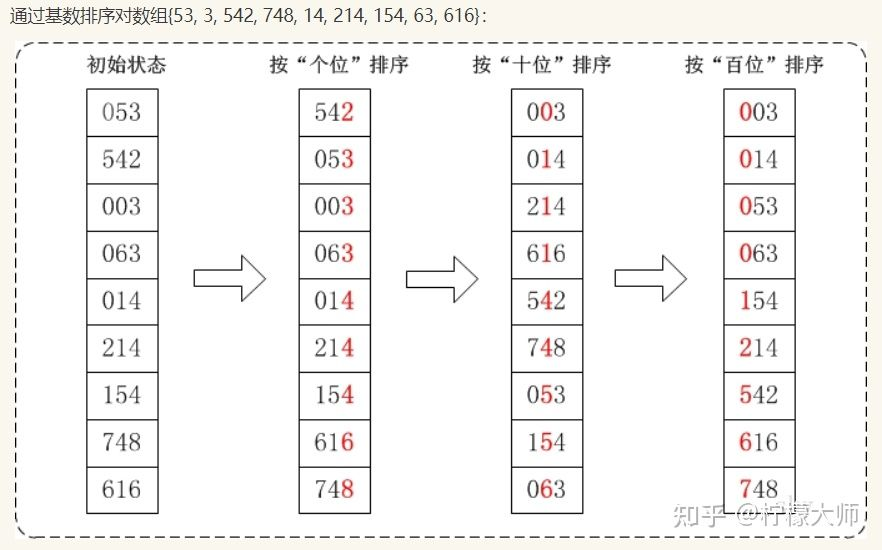
桶排序/基数排序 把数据分组,放在一个个的桶中,然后对每个桶里面分别进行排序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 void RadixSort (int arr[]) int maxNum = arr[0 ]; int len = arr.size (); for (int i = 0 ; i < len; i++) { if (arr[i] > maxNum) { max = arr[i]; } } int size = std::to_string (maxNum).length (); for (int k = 0 , n = 1 ; k < size; k++, n* = 10 ) { int bucket[len][10 ] = {0 }; for (int i = 0 ; i < len; i++) { int temp = arr[i]; int gewei = temp / n % 10 ; bucket[i][gewei] = temp; } int t = 0 ; for (int i = 0 ; i < 10 ; i++) { for (int j = 0 ; j < len; j ++) { if (bucket[j][i] != 0 ) arr[t++] = bucket[j][i]; } } } }
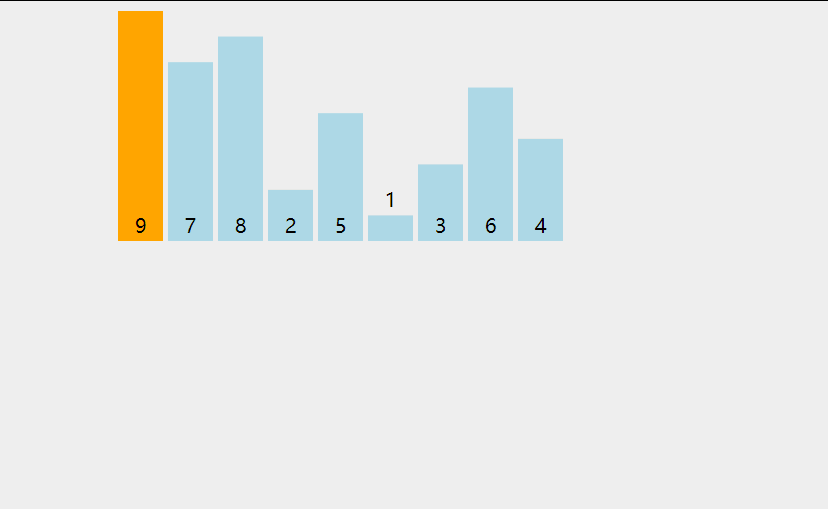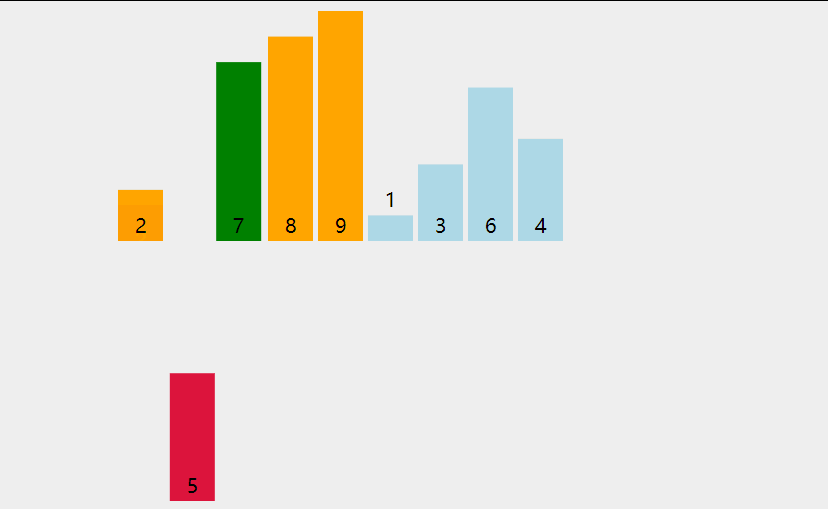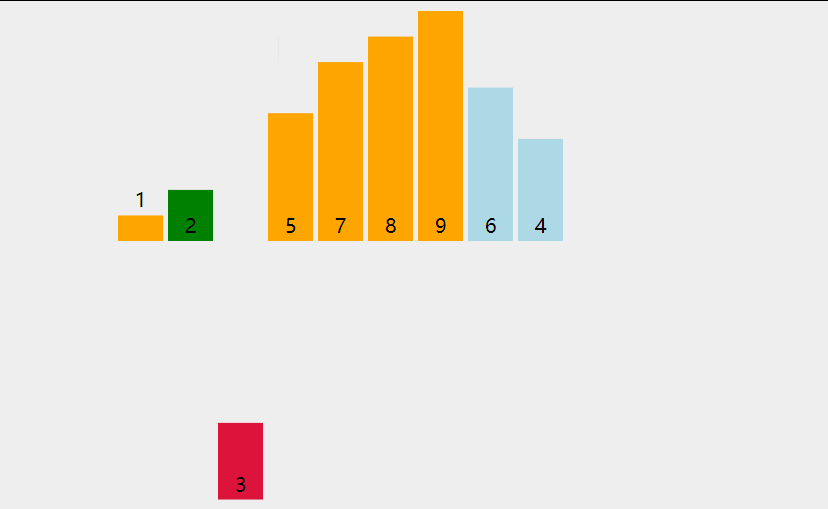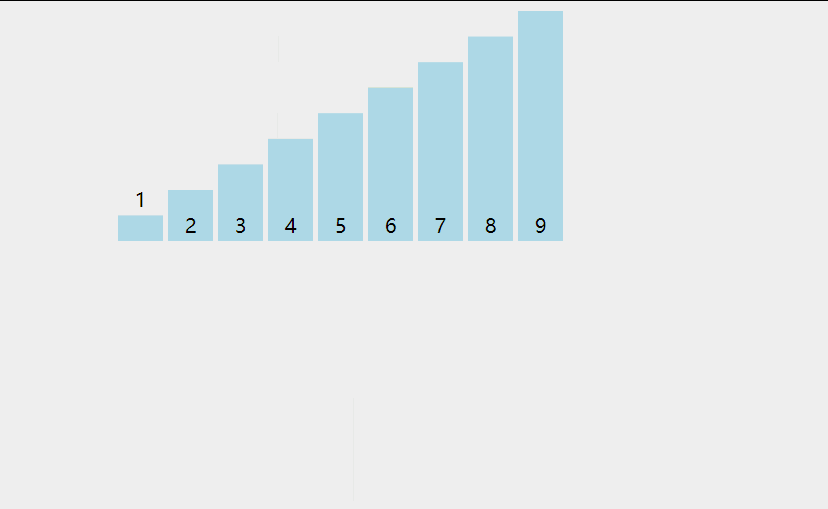
![![]{}](/2022/09/01/%E5%B8%B8%E8%A7%81%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95%E5%AF%B9%E6%AF%94/6613c382-2362-11eb-a750-d6c52a23d5aa.gif)