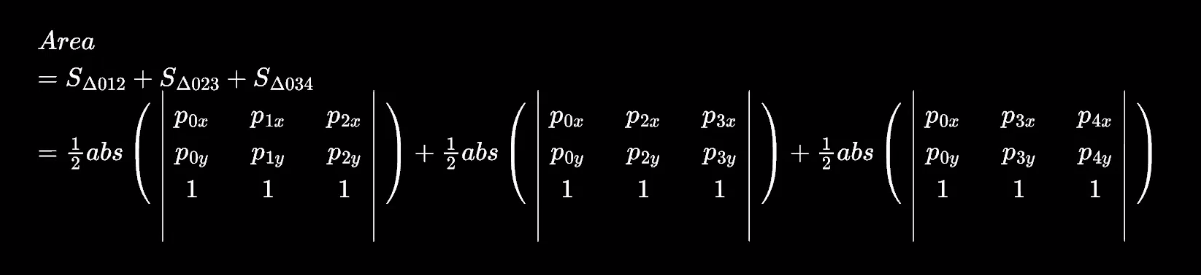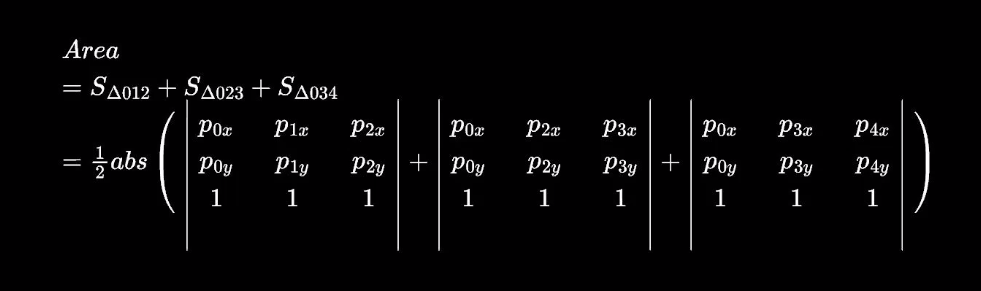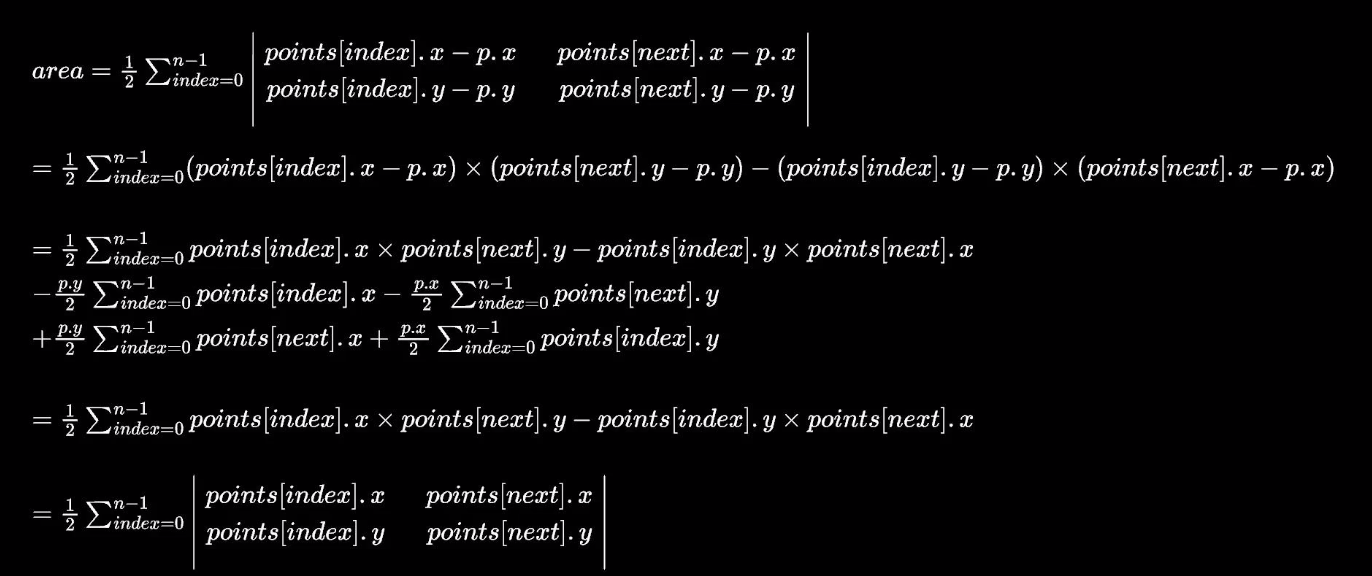计算任意多边形面积

发表于 分类于

首先从简单的使用两个向量计算三角形面积进行推导，找到通过分解多边形为三角形进行计算的方法，再通过数学推导出简单通用的公式。

在计算凸多边形面积时，将凸多边形任取一点与不相邻点连接，将图形分解成多个三角形，使用三角面积公式求和即得。

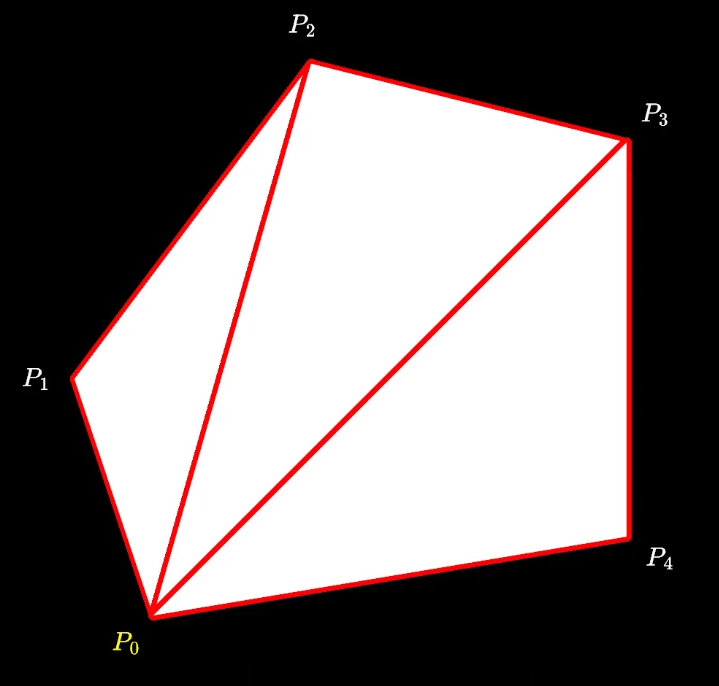
image-20230131001543243

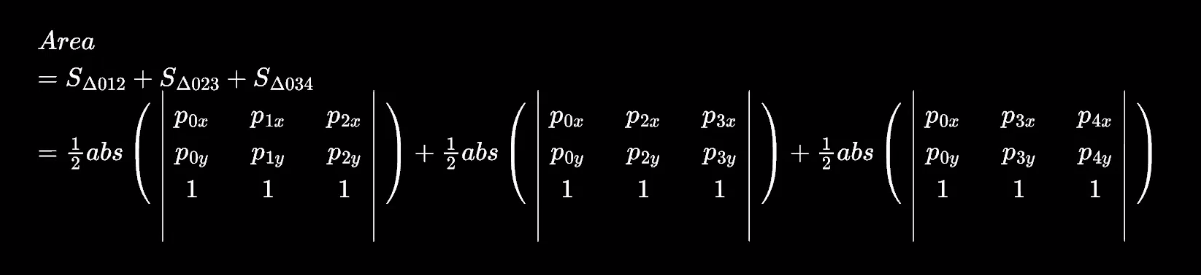
image-20230131001611791

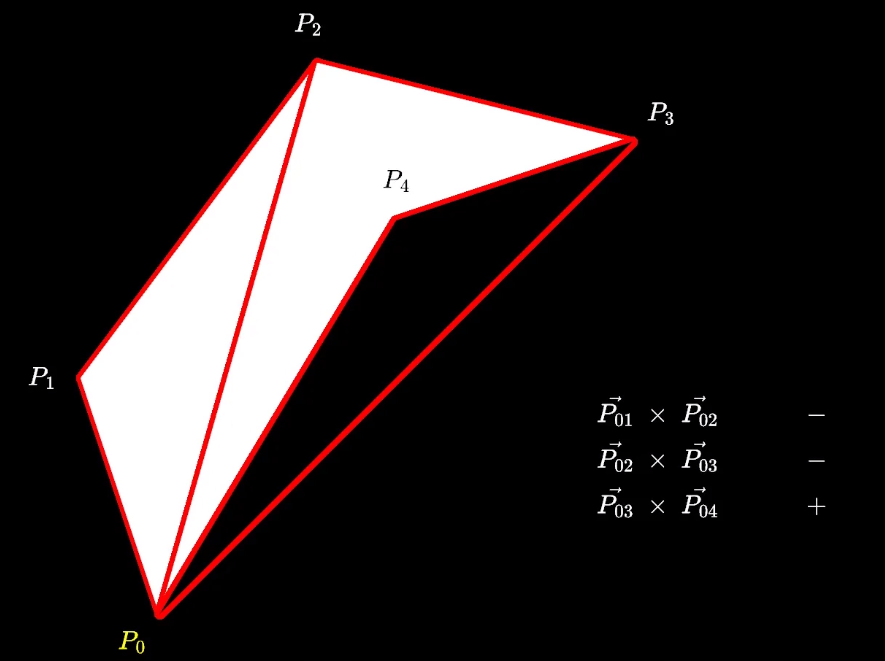
在计算凹多边形面积时，任取一点连续分割出的三角形面积相加不一定能得到正确的面积，但在分割后，可以通过向量叉乘的正负号确定正负，相加得到的总和取绝对值就是面积。

image-20230131002408410

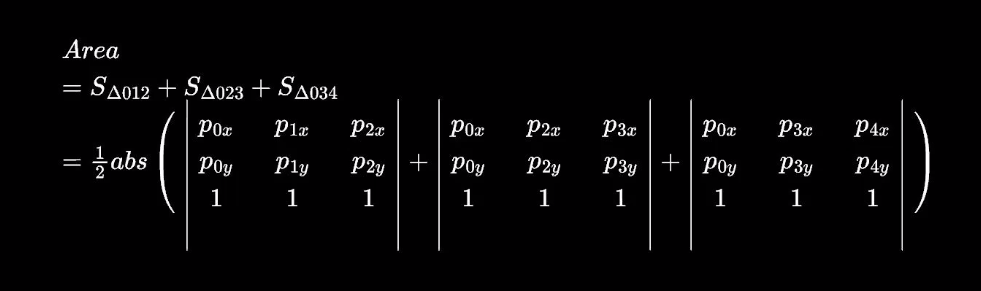
image-20230131002432721

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
struct points {
	double x, y;
};

vector<points> Points;
double x0 = Points[0].x, y0 = Points[0].y, sumArea = 0;
for(int i = 1; i < Points.size() - 1; i ++) {
	double triangle = x0 * Points[i].y
					  + Points[i].x * Points[i + 1].y
					  + Points[i + 1].x * y0
					  - x0 * Points[i + 1].y
					  - Points[i].x * y0
					  - Points[i + 1].x * Points[i].y;
	sumArea += triangle;
}
return abs(sumArea / 2.0);

很明显，第二步中的方法可以计算任意多边形的面积了，但观察到其中是取的任意一点进行分割，这说明这个点的位置可以在多边形内部任意地方，那么这个点的所有信息一定可以在计算中消去。

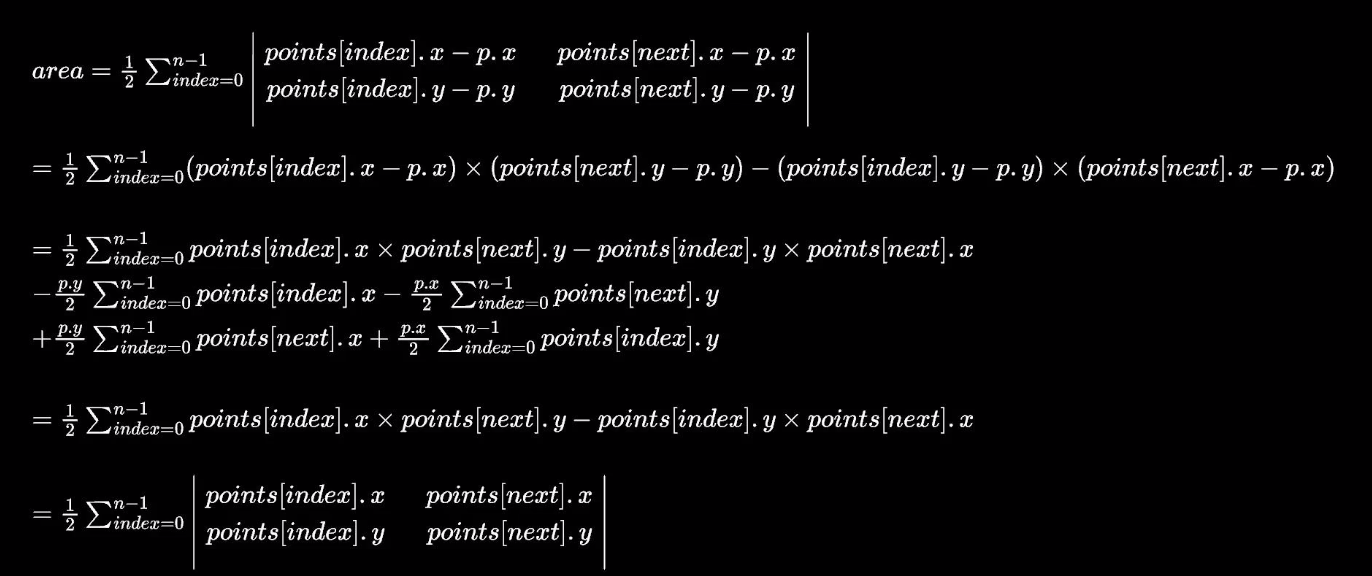
image-20230131010121002

这个数学公式叫鞋带公式。

image-20230131010218415